(Investigation of the myth about high scopes and canting error, in English language see here.)
Írta: Fekete-Móró András
BEVEZETŐ
Annyiszor hallottam már öreg lövőktől, hogy 'a magas távcső nem jó, mert sokkal érzékenyebb a puska oldalra döntésére...' – Ismerősen hangzik? Első pillantásra valóban logikusnak tűnik – de csak amíg egy kicsit alaposabban meg nem vizsgáljuk.
Még 2007-ben kezdtem el foglalkozni ezzel a témával, mikor még 7,5 J-os puskával lőttem és meglehetősen magasra szerelt távcsövet használtam (akkoriban 50 méterig lőttünk a gyenge puskákkal is). Többen mondták, hogy 'Ó, fiam, csak szopni fogsz ezzel a magas szerelékkel és elmegy a lövésed a legkisebb megdöntéstől is, mert a magas távcsövek jóval érzékenyebbek a dőlési hibákra, minden lövész azt tanácsolja, hogy szereld olyan alacsonyra, amennyire csak lehet.'
I. rész – TÉVHITEKRŐL ÉS TÉNYEKRŐL
1. – A tévhitek
Na, jó – mondtam magamnak – lássuk hát, milyen érzékeny a magas távcső a dőlésre. Egy idős fegyvermester a következő módon indokolta ezt nekem, ez a legegyszerűbb hibás érvelés, ami azt mondja, hogy a magas távcső nagyobb oldalirányú elmozdulással jár, ha ugyanakkora szögben megdöntjük a puskát:
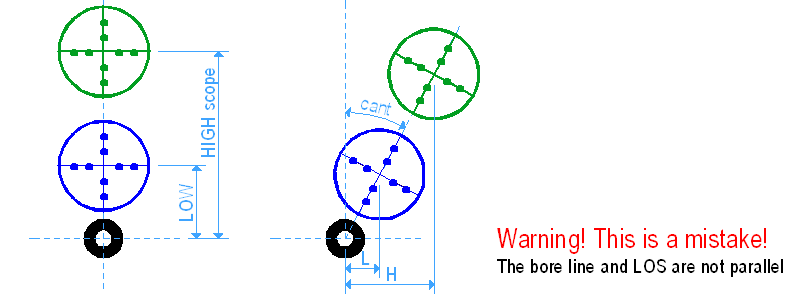
Természetesen, ez csak akkor igaz, ha a lőlap közvetlenül a puska csöve előtt van. A cső vonala és az irányzóvonal nem párhuzamosak egymással a térben, és a különböző magasságú távcsövek irányzóvonalai mind metszik egymás a cél síkjában, így az dőlésből eredő hiba is ugyanakkora (ld. III/1. pont) Aztán találtam egy cikket a témáról az interneten, de meglehetősen zavaros magyarázatokat adott, egy-két helyen pirossal kijavítottam:
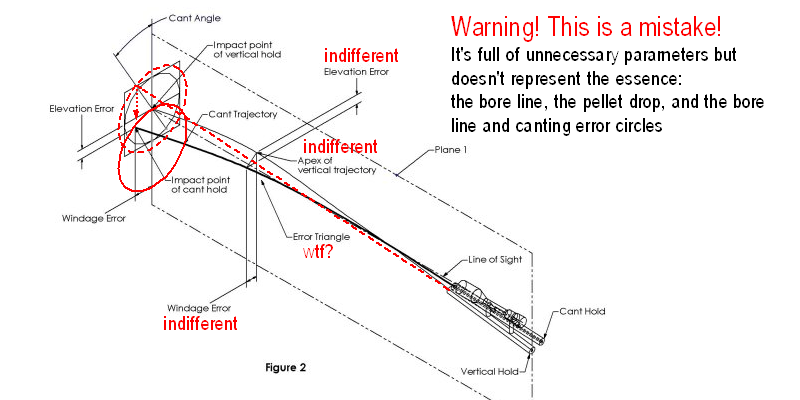
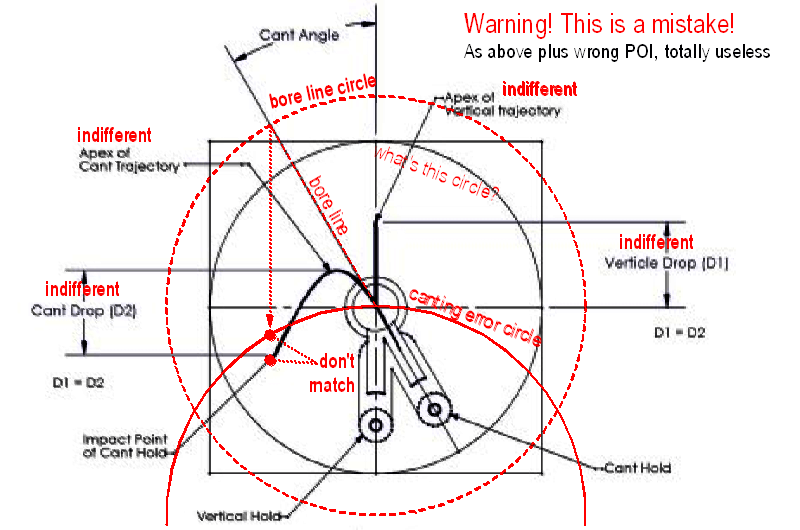
A szerző tökéletesen felesleges paramétereket jelöl meg, mint a röppálya tetőpontja és az innen mért lövedékesés, vagy egy úgynevezett hibaháromszög, ezeknek semmi közük a dőlési hibához. Cserébe viszont kihagyta a lényeget, a cső vonalát és a hibaköröket.
Voltak más tévedések is a cikkben, és a szerző arra a következtetésre jutott, hogy 'Nagy objektívátmérőjű távcsövek használata, a csőtől távol magasan szerelve, súlyosbítja a dőlési hiba problémáját.' Sajnálatos módon, más weboldalak is mint például ez itt mindenféle kritika nélkül átvették ezeket a képeket és magyarázatokat. Láttam már, hogy valami itt nem egészen stimmel és az internetes anyagokban nem lehet feltétlenül megbízni.
Ezért aztán nekiálltam és kidolgoztam a ballisztikai modellt, az alapoktól indulva és meglepetten tapasztaltam, hogy a puska oldalra döntéséből eredő hiba kiszámításához csak a távolság, a lövedék adatai és a dőlés szöge kellenek, a távcső magassága egyáltalán nem szerepel a képletben. Alaposan leellenőriztem és igaznak bizonyult. Itt volt az ideje elkezdeni kísérletezni, hogy végképp eldőljön, kinek van igaza...
2. – Az első kísérleteim (2007)
Így hát, rajzoltam egy kört egy papírlapra az előre kiszámított sugárral, fogtam a puskámat (Walther LG-210, 7,5 J) és lőni kezdtem a kör tetejére mindenféle irányokban megdöntött puskával. A találatok nagyjából mind a körön landoltak, csak a szél fújta el egy kicsit balra az egészet. Összességében azt tapasztaltam, hogy a találatok követték a kört.
Aztán beltérben, 11 méteren próbálkoztam: lőttem a 9 cm magas távcsővel és aztán egy 2 cm magas (CTC) diopterrel. Ez utóbbival sajnos elég gyenge szórást lőttem, erősen elment balra minden lövés. A távcsővel leadott lövések persze megint az előre kalkulált körre érkeztek – a következtetésem az volt, hogy az elméletem működik (a találatok az előre kiszámított kör mentén helyezkedtek el), a diopteres lövés viszont nem az én műfajom...
3. – Hiteles weboldalak a dőlési hibáról
Természetesen, nem én vagyok az egyetlen a világon, aki nem csak szajkózta a régi legendát, hanem el is gondolkodott rajta.
Ott van például Jeroen Hogema, aki lényegében ugyanazt a kísérletet végezte el 1999-ben, mint én. Ő is tesztelte a lövést különböző irányzóvonal-magasságokkal és azt találta, hogy a dőlési hiba nem függ a távcső magasságától.
Egy másik nagyon korrekt és informatív weboldal szerzője Perry Babin, itt egy csomó interaktív Flash animációban magyarázza ez a ballisztikát. A megdöntési hibát bemutató weboldala is tökéletes.
II. rész – ÚJABB KÍSÉRLETEK (2012)
Nem is foglalkoztam többet ezzel a kérdéssel, felszereltem a távcsövemet egy szép kényelmes magasságba és magasról tojtam az aggodalmakra. Nemrég azonban, miután nagykaliberű puskás kollégákkal beszéltem róla, újra át kellett gondolnom és találtam egy kivételt a szabály alól: vannak bizonyos speciális esetek, amikor a magas távcső többé vagy kevésbé érzékeny a puska megdöntésére, mint az alacsony. Ezért úgy gondoltam, érdemes lenne egyszer 's mindenkorra tisztázni ezt a kérdést.
Első lépésként megismételtem az első kísérletemet. Fogtam Ágicza puskáját és kiszámoltam 21 méterre a hibakör átmérőjét. Aztán lőttem különböző dőlésekkel és a lövedékek ismét csak a kör mentén csapódtak be. Ez már magában is bizonyíték volt, hiszen nem használtam fel a távcső magasságát a számításokhoz, ezért ugyanazt az eredményt kaptam volna más távcsőmagassággal is.
Megpróbáltam lőni egy kis átmérőjű, nagyon alacsonyra szerelhető távcsővel (4x-es 'lepkekergető'), de azt kellett tapasztalnom, hogy 3-4 cm-es körben lövök vele és csak megismételném azt a hajdani, sörétes puskát is megszégyenítő diopteres szórásképet. Ezért úgy döntöttem, Ági pontos és nagy nagyítású távcsövét fogom használni mindkét magassághoz és a jelentős magasságkülönbséget a másik irányban fogom elérni, ipari mennyiségű távcsőmagasító használatával. A másik fontos tapasztalatom az volt, hogy egy ingatag kerti padról lőni nem túl stabil és valami sokkal jobbat kell találnom, ha értékelhető eredményeket szeretnék kapni. Lássuk, végül is hogy csináltam:
1. – Előkészületek és körülmények
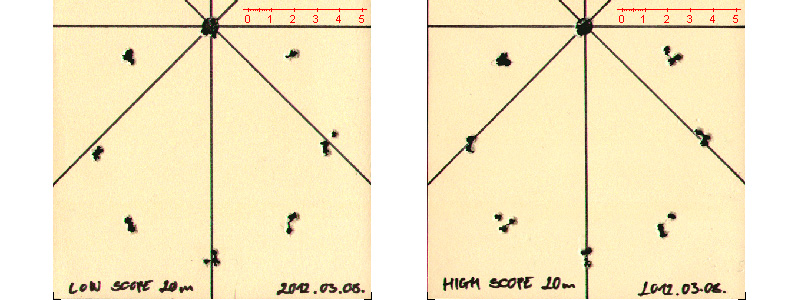
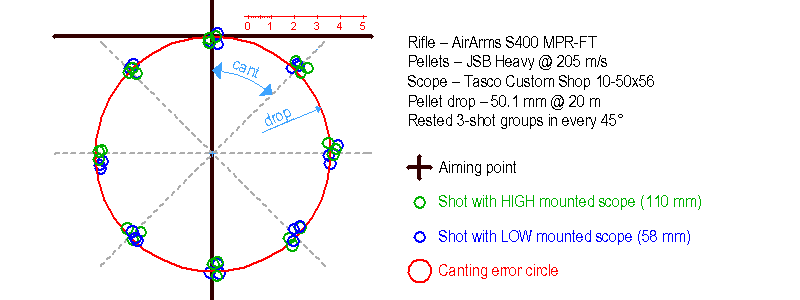
Ágicza AirArms S-400 MPR-FT puskáját használtam, ez eredeti gyári állapotú a lengőcsöves kialakítás kivételével, amivel megszüntettem a POI-vándorlást, ami korábban a hőmérséklet vagy a légtartály nyomásváltozása miatt jelentkezett. JSB Heavy lövedékkel lőttem, 205 m/s sebességgel. A számított lövedékesés a 20 méteres távon 50,1 mm volt (úgy választottam a távolságot, hogy a hibakör elég nagy legyen, de minden lövés a papíron maradjon). 3 lövéses csoportokat lőttem minden 45°-os szögben, a puskát egy ülőpárnán megtámasztva. A távcsőmagasság 58 mm és 110 mm volt (CTC).
Azt már tudtam, hogy egy durván megdöntött puskával lőni meglehetősen bonyolult, néha bal szemmel kell célozni és jobb kézzel elsütni vagy fordítva, a puska inog a parallaxkerék tetején és nem lehet rendesen vállba fogni sem, tehát a székről való lövés pontossága valahol a térdelő és az álló lövések között lesz, már ha a szórásképet nézzük...
Ezért valamilyen professzionális lőállást kerestem és meg is találtam azt a Renault Laguna kocsink képében. Talán különös látvány volt, de egy nagyon kényelmes és stabil pozícióból lőhettem a hátsó ülésről, a puskát a kalaptartóra helyezett párnára támasztva. Minden szerszám, légpalack és egyéb kellék ott volt velem a kocsiban. A világ első önjáró lőállása beépített hifivel és klímával, LOL.
Ezek nem az olasz pályaépítéshez kifejlesztett alternatív lőpozíciók, hanem már a tesztelés. Különböző szögekkel döntöttem meg a puskát, a szög méréséhez nem libellát használtam, hanem a lőlapra rajzot 45°-os vonalakhoz igazítottam a szálkeresztet.
Az idő csaknem ideális volt, nagyjából 10 fok, elhanyagolható szellő, nem esett és nem sütött a nap sem. Először belőttem a puskát 20 méterre egy másik lapon, majd 3-3 lövést adtam le 45°-os lépésekben mindkét irányban, végül teljesen fejre állított puskával is lőttem. Aztán kiszedtem a 4-4 magasító sínt és megismételtem az egész folyamatot.
2. – Teszteredmények
A lőlapok meglehetősen hasonlóak lettek, akár további elemzések nélkül is láthatjuk, hogy a csaknem kétszer akkora távcsőmagasság nem eredményezett semmilyen értékelhető különbséget.
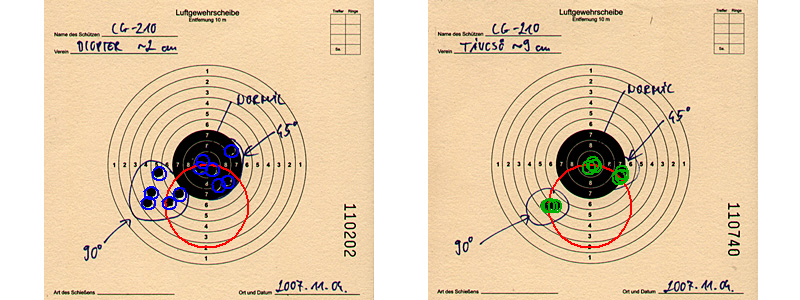
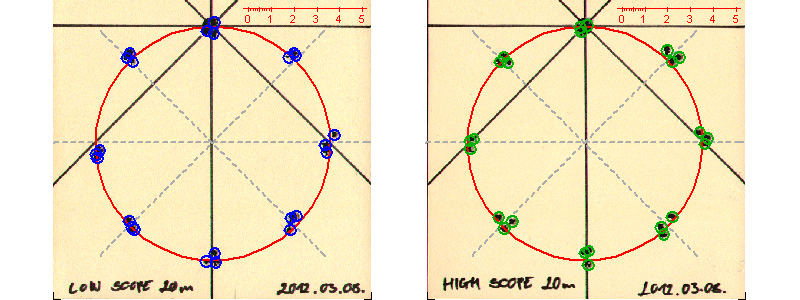
Aztán megjelöltem a lövések helyét 4,5 mm-es kis körökkel és felrajzoltam a számított dőlésihiba-köröket is. Nem túl meglepő módon, minden lövéscsoport a körre esett.
Ez a teszt végeredménye, az egy rajzon egyesített szórásképek. Magáért beszél.
Következtetésem az, hogy a távcső magassága NINCS hatással a dőlési hiba mértékére. Tehát figyelni kell a vízmértéket, drága barátaim, a legalacsonyabb távcsőnél is, mert ez minden távcsőmagasság esetén egyformán fontos.
III. rész – AZ ELMÉLET
1. – Hogy keletkezik a dőlési hiba?
Essen most egy pár szó az eredeti elméletemről (1-2. pont) és annak kiterjesztett változatáról a speciális esetekre (3-4. pont) ahol a távcső magassága mégis számít.
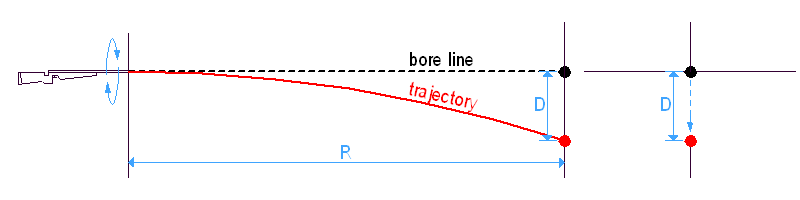
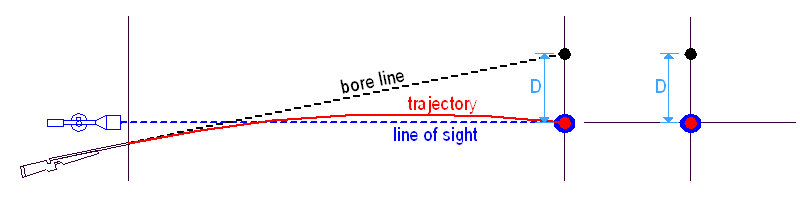
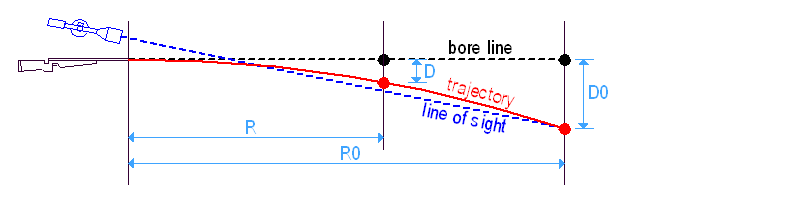
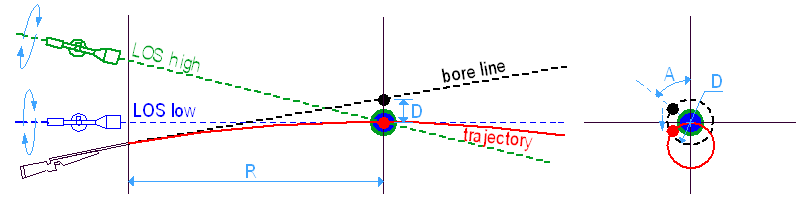
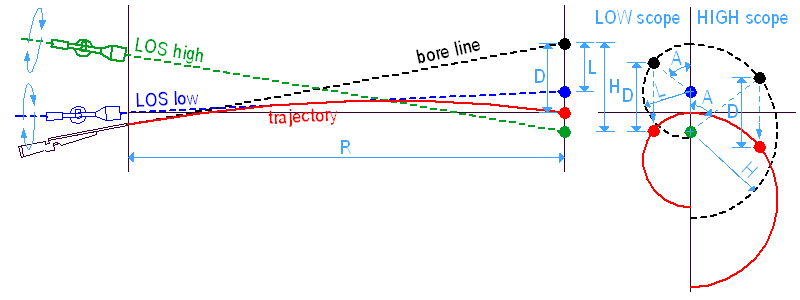
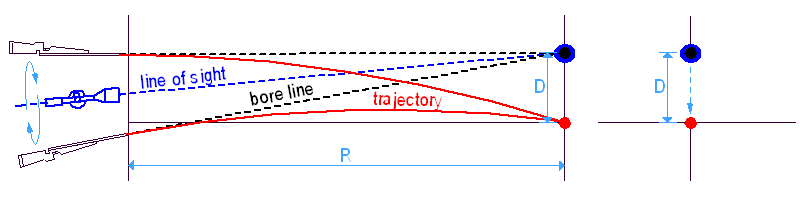
Ha egy 'R' távolságra lövünk, a lövedék esése 'D', ami csak a lövedék V0 és a BC értékeitől függ, a távcső magasságától nem. Bármilyen irányba megdöntött puskával lőhetünk, ahová a puskacső vonala néz a cél síkjában, a lövedék 'D'-vel alatta fog becsapódni.
Így célzunk és lövünk: az irányzóvonal (LOS a rajzon) a célra néz, a csőtengely (bore line) 'D'-vel fölé, így a lövedék (ami ugye 'D'-t esik az adott távon) éppen beletalál a célba.
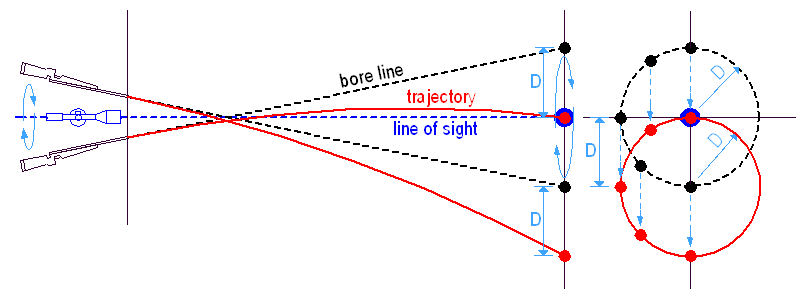
A puska megdöntése célzás közben = a cső elforgatása az irányzóvonal, mint tengely körül. Az elforgatás tengelye mindig a LOS, mert a szálkereszt a célon marad, tehát az egész miskulancia e körül fordul el, mikor fellép a megdöntés. Ez azt jelenti, hogy a cső vonala egy 'D' sugarú kört rajzol a cél köré és a találatok egy ugyanilyen sugarú körön lesznek 'D'-vel alatta (ez a piros kör a lőtesztek eredményein, az ún. hibakör).
Most képzeljünk el egy puskát, amelyen egymás felett két távcső van egymás felett. Mindkét irányzóvonal – magas és alacsony – ugyanabba a pontba néz, így a puskacső is ugyanazt a 'D' sugarú kört rajzolja. Ezért független a dőlési hiba a távcső magasságától, csak a 'D' lövedékeséstől és az 'A' megdöntési szögtől függ.
Vagy ugyanez más képi megfogalmazásban, ha így esetleg könnyebb elfogadni :-)
A vízszintes ill. függőleges dőlési hiba ('Ex' és 'Ey') valamint az abszolút (sugár irányú) eltérés ('Er') az alábbi képletekkel számítható. A 'D' lövedékesést adott távon meg is lehet mérni (ld. III./1. a vége felé), a Chairgun-nal is kiszámítható, vagy egyszerűen használjuk az alábbi képletet:
ahol BC a valódi BC érték, R a távolság yardban, V0 a torkolati sebesség fps-ben, a hiba értékeit és D-t hüvelykben kapjuk meg. Vegyük észre, hogy a távcső magassága nem szerepel a képletben :-)
2. – Más távolság, más irányzóvonal
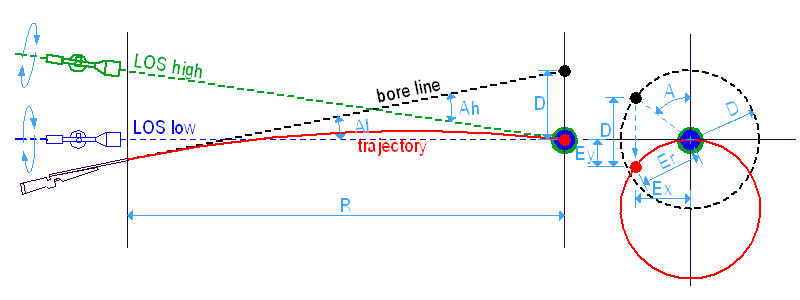
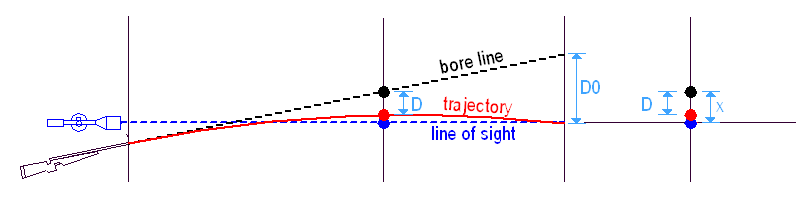
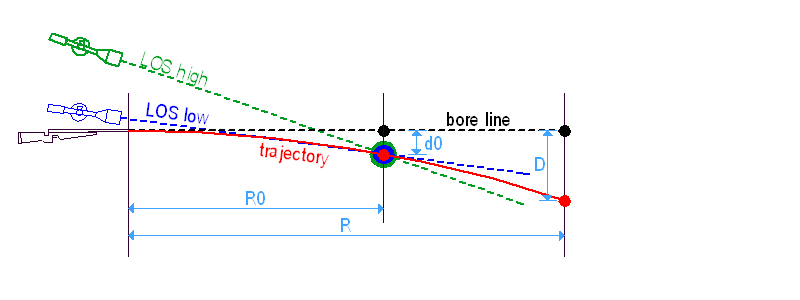
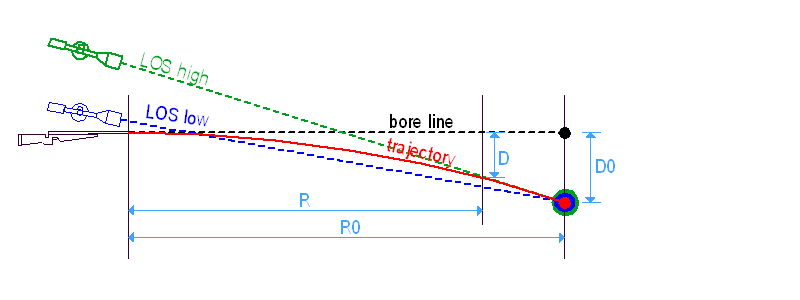
Rendben van, na de mi történik más távolságokon? Vizsgáljunk most meg egy olyan puskát, amit belőttünk egy 'R0' távolságra, de egy másik 'R' távra szeretnénk lőni vele. A lövedékesés az 'R' távolságon 'D' lesz, vagyis ezzel a 'D'-vel kell a puskacsőnek a cél fölé néznie, hogy a lövedék a célba érkezzen.
mivel a LOS egyenes és a röppálya íves, az 'R0' távolságra belőtt puska alá vagy fölé hord (a konkrét ballisztikától függően) az 'R' távolságon, a cső egy másik 'X' értékkel néz a cél fölé a kívánt 'D' helyett. Ha el szeretnénk találni a célt, úgy kell megváltoztatnunk a csőtengely-irányzóvonal szöget, hogy a cső vonala pontosan 'D'-vel nézzen a cél fölé.
Így tehát más távolsághoz más irányzóvonalat kell használnunk. Ezt megtehetjük a távcső magasságállításával illetve mildotos alá/fölétartással. Bárhogyan is, a lényeg az, hogy megváltoztatjuk az irányzóvonalat és az aktuális LOS ismét a célra néz.
Nagyon fontos megértenünk: valójában minden távra be van lőve a puskánk, amire csak lövünk.
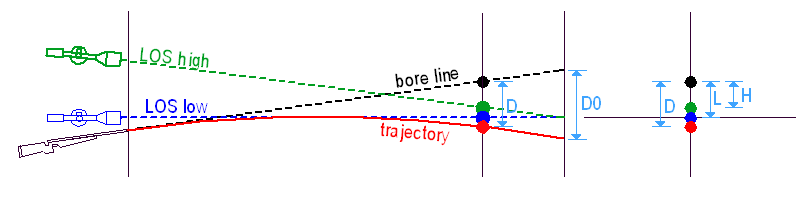
Most pedig nézzük ismét a két távcsővel felszerelt puskát. Az 'R' távolságra lőve, az alacsony és magas távcső új irányzóvonala is a célra néz, így a lövések ugyanazon a 'D' sugarú körön lesznek. A távcső magasságának megint csak nincs hatása a dőlési hibára, az csak a megdöntés 'A' szögétől és a 'D' lövedékeséstől függ az adott 'R távolságon'.
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
Ám most jön a csavar a történetben, kedves ápolttársak, kérjük a biztonsági öveket becsatolni... Mi a Field Target-ben gyakorlatilag minden egyes távolságra belőjük a puskánkat. Még egyszer mondom, még a mildotokkal való lövés is egyfajta zérózást jelent az adott távolságra. Tehát bárhogyan is célzunk, az irányzóvonalunk mindig a célra néz és ha megdöntjük a puskát, a csőtengelyt a cél körül forgatjuk, a fent részletezett eredményekkel.
Feltűnt azonban, hogy az összes efféle 'a magas távcső rossz' véleményt a nagy távolságokra, golyós puskákkal lövőktől eredeztethető. Lehetséges-e, hogy ők valamit másként csinálnak és ez megváltoztat bizonyos dolgokat az elméletben? És igen, így van. Felül kellett vizsgálnom az eddigi álláspontomat. Az összes eddigit természetesen fenntartva, megvizsgáltam egy harmadik célzási módszert, amikor a lövő egy másik pontba céloz a cél felett vagy alatt, melynek a távolságát a célon méri ki.
3. – Amikor a magas távcső hátrányosabb
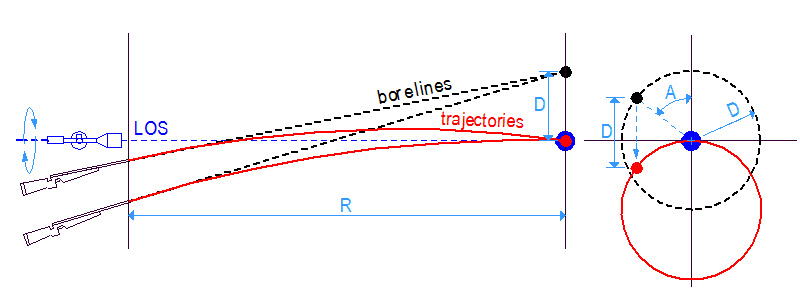
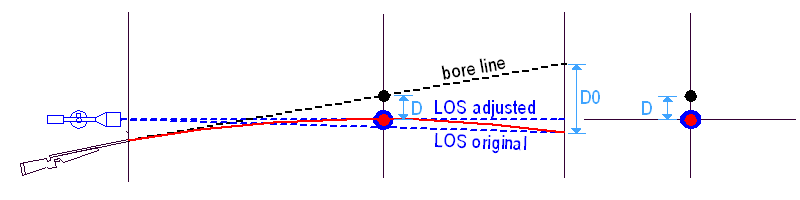
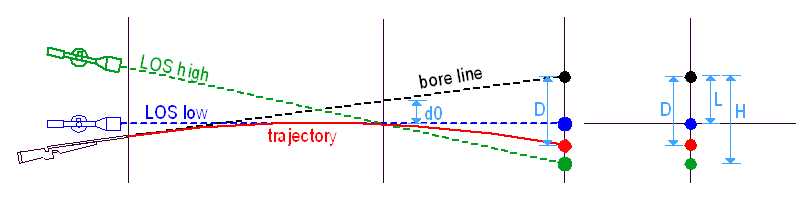
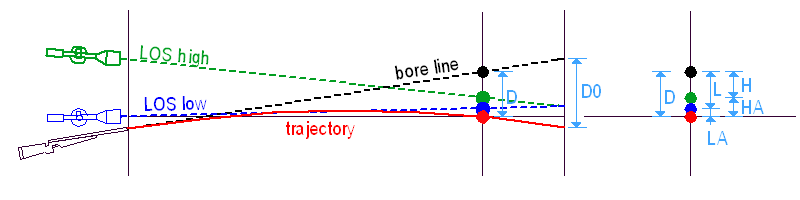
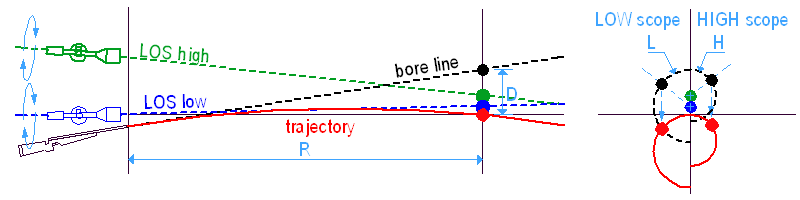
Ezúttal két távcső van a puskánkon, egy alacsony és egy magas. Mindkét távcső be van lőve az 'R0' távolságra, de mi egy másik 'R' távra lövünk, amin 'R0'-nál TÁVOLABB van.
Az 'R0'-ra belőtt puska nem talál célba az 'R' távolságra lőve, mert a csőtengely más értékkel néz a cél fölé, 'L'-lel az alacsony és 'H'-val a magas távcső, a kívánt 'D' helyett. Bizonyos esetekben előfordulhat, hogy 'L' vagy 'H' egyenlő 'D'-vel, de ez a ritka kivétel (csak akkor történik meg, ha 'R0' és 'R' az aktuális röppálya-irányzóvonal együttes két nullpontja). A piros, kék és zöld pontok egymáshoz viszonyított helyzetet változhat a ballisztikai adatokkal, de 'L' mindig KISEBB, mint 'H'.
Ezért hát egy olyan pontra célzunk a szálkereszttel, amely a célpont alatt/felett helyezkedik el, a megfelelő 'LA' ill. 'HA'távolságra. A cső e fölé néz 'L' ill. 'H' értékkel és mindkét esetben 'D'-vel néz a cél fölé, így a 'D' esésű lövedék a célba talál.
Ha megdöntjük a puskát, a csőtengely természetesen megint az irányzóvonal körül fordul el – de ezzel a célzási móddal ez két különböző pontot jelent! Ezért a hibakör sugara 'D' helyett 'L' lesz az alacsony távcsővel és 'H' a magassal. Mivel pedig 'H' nagyobb 'L'-nél, a magasabb távcsővel lőve NAGYOBB lesz a dőlési hiba.
4. – Amikor a magas távcső előnyösebb
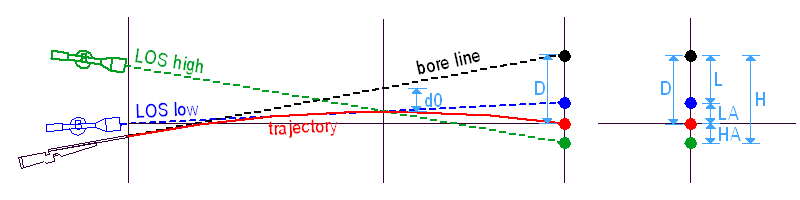
És most lássuk a fenti eset fordítottját. Most is két távcső van a puskánkon, egy alacsony és egy magas. Mindkét távcső be van lőve az 'R0' távolságra, de mi egy másik 'R' távra lövünk, amin 'R0'-nál KÖZELEBB van.
Az 'R0'-ra belőtt puska nem talál célba az 'R' távolságra lőve, mert a csőtengely más értékkel néz a cél fölé, 'L'-lel az alacsony és 'H'-val a magas távcső, a kívánt 'D' helyett. A piros, kék és zöld pontok egymáshoz viszonyított helyzetet változhat a ballisztikai adatokkal, de 'L' mindig NAGYOBB, mint 'H'.
Ezért hát egy olyan pontra célzunk a szálkereszttel, amely a célpont alatt/felett helyezkedik el, a megfelelő 'LA' ill. 'HA'távolságra. A cső e fölé néz 'L' ill. 'H' értékkel és mindkét esetben 'D'-vel néz a cél fölé, így a 'D' esésű lövedék a célba talál.
Ha megdöntjük a puskát, a csőtengely természetesen megint az irányzóvonal körül fordul el – de ezzel a célzási móddal ez két különböző pontot jelent! Ezért a hibakör sugara 'D' helyett 'L' lesz az alacsony távcsővel és 'H' a magassal. Mivel pedig 'H' kisebb 'L'-nél, a magasabb távcsővel lőve KISEBB lesz a dőlési hiba.
5. – Hogyan kerüljük el a dőlési hibát?
1. Tartsuk 0-n a megdöntés szögét. Ez a legegyszerűbb megoldás, csak egy pontosan beállított libella kell hozzá és nincs több dőlési hiba! Ez így túlságosan is egyszerű? Vannak más megoldások is:
2. Csökkentsük a lövedékesést. Könnyebb lövedékkel és ezáltal nagyobb sebességgel lőve a 'D' értéke csökken és ezzel csökken a hibakör sugara, végső soron maga a hiba is.
3. Ha gyűlölöd a vízmértékeket, nem szeretnél más lövedékkel lőni, ellenben kened-vágod a ballisztikát, van még egy (bár inkább elméleti) lehetőség is a megdöntésből eredő hibák elkerülésére: csökkentsd 0-ra a hibakör sugarát, így a szög már nem fog számítani. Hogy lehet ezt elérni? Lődd be úgy a puskád, hogy a csőtengely és az irányzóvonal a cél síkjában metssze egymást. Természetesen, célozz 'D'-vel a cél fölé. Ily módon bármilyen szögben elforgathatod a puskát, a hibakör sugara 0, így 0 lesz a hiba mértéke is... :-)
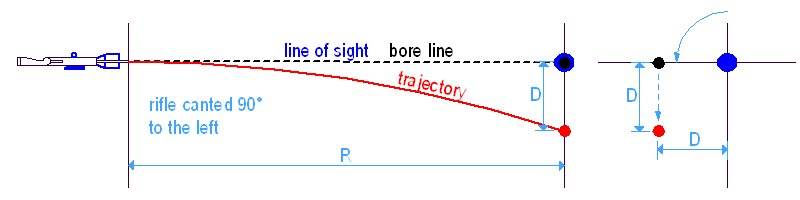
Egy másik példa új ismereteink felhasználására: ha szeretnéd megtudni a lövedékesésedet egy adott távolságon, egyszerűen lődd be a puskát az adott távra, majd fordítsd el 90 fokkal balra és lőj vele úgy. A találat pontosan 'D'-vel lejjebb és 'D'-vel balra lesz.
IV. rész – ÖSSZEFOGLALÁS
1. Általánosságban, és különösen az FT lövészetben, ahol az irányzóvonal szükséges korrekcióját a távcsövön belül valósítjuk meg (clickeléssel állítva a távcsövön vagy mildotokkal célozva), a puska megdöntéséből eredő hiba tökéletesen független a távcső magasságától, a magasabb távcsövek NEM érzékenyebbek a megdöntésre, mint az alacsonyabbak.
2. Ha a korrekciót a távcsövön kívül hajtjuk végre (vagyis a célon mért távolságokkal tartunk alá/fölé lövéskor), a megdöntésből eredő hiba eltérő – kisebb vagy nagyobb – a magas távcsővel. Nagyobb lesz, ha a cél távolsága nagyobb a zéró távolságnál és kisebb, ha a távolság is kisebb.
Mivel az FT-ben engedélyezett a libella használata, a puska oldalirányú dőlése nem igazi probléma számunkra. És, amint a fentiekből kiderült, rakhatod olyan magasra a távcsövet, amilyenre csak akarod, nem lesz érzékenyebb a dőlésre. Sokkal fontosabb viszont, hogy az alacsony távcsővel lövőknek is ugyanúgy oda kell figyelniük a puska vízszintben tartására, mert az ő puskájuk ugyanolyan érzékeny a megdöntésre, mint a magas távcsővel lövőké.
Bár a puska dőléséről kiderült, hogy független a távcső magasságától, a magas távcsőnek vannak bizonyos előnyei és hátrányai:
Előnyök:
– laposabb röppálya a nagyobb távolságokon, több tévedést enged a távmérésben
– kényelmesebb, egyenesebb fejtartást tesz lehetővé
– több hely marad a puska töltésére
Hátrányok:
– közeli távokon meredekebb röppálya, kifogyhatunk a clickekből
– nagyobb esély a földbe/ágba lövésre szabálytalanul épített pályák esetén
Ezeket a szempontokat mind figyelembe kell vennünk a távcső magasságának meghatározásakor, de a dőlési hiba nincs közöttük – remélhetőleg végleg megszabadultunk ettől a tévhittől.





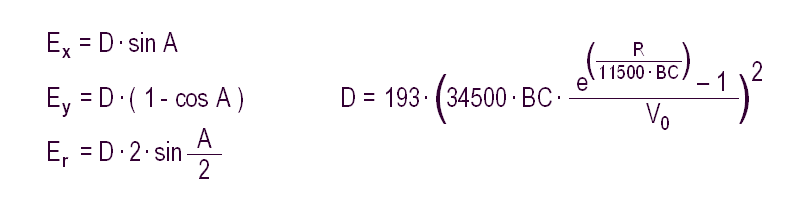
2 komment:
Köszönöm a munkádat!
Insurgent
Köszönöm a hasznos információkat. Az LG 210-es csonkítás nélküli távcsövesítése vonatkozásában is.
Joe
Megjegyzés küldése